Μεγέθη κινηματικής
Επειδή στα σχολικά, και όχι μόνον, βιβλία μερικά από τα βασικά μεγέθη κινηματικής δεν αποσαφηνίζονται πλήρως ή παρουσιάζονται με λανθασμένο τρόπο ή μπερδεύονται μεταξύ τους με συνέπεια να δημιουργείται σύγχιση, αλλά και να χρησιμοποιείται άλλο μέγεθος αντί άλλου, καταθέτω προς συζήτηση μερικές απόψεις αποσαφήνισης
Θέση x (ή διάνυσμα θέσης)
Πρόκειται για διάνυσμα που αρχίζει από το σημείο αναφοράς (ή αφετηρία, που επιλέγεται αυθαίρετα) και τελειώνει στο υλικό σημείο (ή στο κέντρο μάζας στερεού)
Προφανώς η θέση εξαρτάται από το σημείο αναφοράς που επελέγη
Μετατόπιση Δx
Πρόκειται για διάνυσμα που αρχίζει από την αρχική (γεωμετρική) θέση ενός υλικού σημείου και τελειώνει στην τελική (γεωμετρική) θέση του
Η μετατόπιση υπολογίζεται από τη διανυσματική διαφορά xτελ-xαρχ και δεν εξαρτάται από το σημείο αναφοράς (ευτυχώς, διότι άλλως δεν θα μπορούσαμε να συνεννοηθούμε μεταξύ μας)
Απόσταση d δυο σημείων
Πρόκειται για μονόμετρο μέγεθος ίσο με το μέτρο του διανύσματος που αρχίζει από το ένα σημείο και τελειώνει στο άλλο
Μήκος διαδρομής s
Πρόκειται για μονόμετρο μέγεθος ίσο με το μέτρο της μετατόπισης αν η διεύθυνση κίνησης παραμένει σταθερή ή για το άθροισμα των μέτρων των επί μέρους μετατοπίσεων αν η διεύθυνση κίνησης μεταβάλλεται (το μήκος της διαδρομής δεν είναι πάντα ίσο με το μέτρο της μετατόπισης, για παράδειγμα όταν ένα κινητό διαγράφει μια πλήρη κυκλική διαδρομή το μήκος της διαδρομής είναι 2πR και το μέτρο της μετατόπισης είναι 0, και κάποιες φορές είναι πιο χρήσιμο, πρακτικά, απ' αυτό, για παράδειγμα όταν ένα αυτοκίνητο πραγματοποιήσει τη διαδρομή Αθήνα-Νεάπολη Λακωνίας-Αθήνα 33 φορές το μήκος της διαδρομής δείχνει το κόστος ενώ το μέτρο της μετατόπισης δεν δείχνει τίποτα αφού είναι 0 )
Διάστημα s (;)
Πρόκειται για μονόμετρο μέγεθος που άλλοτε χρησιμοποιείται ως μέτρο της μετατόπισης και άλλοτε ως μήκος διαδρομής (και που, καλό θα είναι, να πάψει να χρησιμοποιείται εντελώς)
Βαγγέλης Κουντούρης
(ΥΓ: πρόκειται για μια πρώτη ανάρτηση, αν τα καταφέρω, που γίνεται σύμφωνα με τις οδηγίες που δημοσιεύει, για όλους εμάς τους αδαείς, ο συνάδελφος Νίκος Ανδρεάδης, τον οποίο και ευχαριστώ, γι' αυτό και ζητείται η κατανόηση σας)
Κυριακή 27 Δεκεμβρίου 2009
Τρίτη 15 Δεκεμβρίου 2009
Ένα Test στη Δυναμική-κατακόρυφη βολή.
Ένα σώμα μάζας 3kg ηρεμεί στο έδαφος. Σε μια στιγμή t0=0, ασκούμε πάνω του, μέσω νήματος, μια σταθερή κατακόρυφη δύναμη μέτρου F=42Ν, με αποτέλεσμα το σώμα να αρχίζει να ανέρχεται. Τη χρονική στιγμή t1=5s το νήμα κόβεται.
i) Με πόση επιτάχυνση κινήθηκε το σώμα για όσο χρόνο του ασκήθηκε η δύναμη F;
ii) Σε πόσο ύψος από το έδαφος βρισκόταν το σώμα τη στιγμή που κόπηκε το νήμα;
iii) Ποιο είναι το μέγιστο ύψος στο οποίο θα φτάσει το σώμα;
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s2.
Μονάδες 8+5+7=20
Ετικέτες
2. Δυναμική,
8. Τest,
Διονύσης Μάργαρης
Κατακόρυφη Βολή.
Τι κάνουμε λοιπόν όταν έχουμε μια εκτόξευση με κάποια αρχική ταχύτητα, ενός σώματος σε κατακόρυφη διεύθυνση;
Παίρνουμε τον κατακόρυφο άξονα y΄y και αφού θέσουμε κάπου το μηδέν του άξονα (συνήθως στο σημείο εκτόξευσης) ορίζουμε την θετική φορά του άξονα. Βολεύει να παίρνουμε την κατεύθυνση της αρχικής ταχύτητας εκτόξευσης ως θετική.
Κατόπιν με βάση τα προηγούμενα και αφού το σώμα έχει σταθερή επιτάχυνση, γράφουμε τις εξισώσεις της ευθύγραμμης πμαλά μεταβαλλόμενης κίνησης.
Ας το δούμε με κατάλληλα παραδείγματα.
Παράδειγμα 1ο:
Από ύψος Η=25m από το έδαφος εκτοξεύεται τη χρονική στιγμή t0=0, κατακόρυφα προς τα πάνω, ένα σώμα με αρχική ταχύτητα μέτρου υ0=20m/s. Αν g=10m/s2 και η αντίσταση του αέρα θεωρείται αμελητέα, ζητούνται:
- Η ταχύτητα και η θέση του σώματος τη χρονική στιγμή t1=1s.
- Η ταχύτητα και η θέση του σώματος τη χρονική στιγμή t1=3s.
- Ποια χρονική στιγμή και με ποια ταχύτητα το σώμα φτάνει στο έδαφος;
Απάντηση:
Στο διπλανό σχήμα έχει σχεδιαστεί ο κατακόρυφος άξονας y΄y πάνω στον οποίο πραγματοποιείται η κίνηση, με θετική φορά προς τα πάνω και με το σημείο εκτόξευσης Ο στη θέση y=0.
Το σώμα έχει σταθερή επιτάχυνση α= -g, αφού η επιτάχυνση του σώματος έχει φορά προς τα κάτω. Έτσι οι εξισώσεις για την κίνηση του σώματος είναι:
υ= υ0 + α·t → υ=υ0-gt (1) και
Δy= υ0·t + ½ α·t2 → y= υ0·t – ½ g·t2 (2)
1) Αντικαθιστώντας στις παραπάνω σχέσεις t1=1s παίρνουμε:
υ1 = υ0-gt=20m/s-10m/s2·1s= 10m/s.
y1 = υ0·t – ½ g·t2 = 20·1- ½ 10·1= 15m.
Δηλαδή το σώμα συνεχίζει να κινείται προς τα πάνω με ταχύτητα μέτρου 10m/s ενώ βρίσκεται πιο ψηλά από την αρχική του θέση κατά 15m. Ή αν θέλετε έχει μετατοπισθεί κατά 15m και βρίσκεται πλέον σε ύψος:
h=Η+y= 25m+15m=40m.
2) Με αντίστοιχη αντικατάσταση για t2=3s παίρνουμε:
υ2 = υ0-gt=20m/s-10m/s2·3s= -10m/s.
y2 = υ0·t – ½ g·t2 = 20·3- ½ 10·32= 15m.
Τι βρήκαμε; Το σώμα έχει τώρα ταχύτητα μέτρου 10m/s, με φορά προς τα κάτω, ενώ βρίσκεται ξανά 15m πάνω από το σημείο εκτόξευσης. Είναι δηλαδή στην ίδια θέση που ήταν και για t1=1s.
3) Τη στιγμή που το σώμα φτάνει στο έδαφος έχει απομάκρυνση y= -25m και με αντικατάσταση στην σχέση (2) θα έχουμε:
y= υ0·t – ½ g·t2 → -25 = 20t – ½ 10·t2 ή
5t2 -20t-25=0 ή
t2 -4t-5=0
Συνεπώς ή t= -1s (απορρίπτεται) ή t=5s (δεκτή λύση)
Και με αντικατάσταση στην (1) έχουμε:
υτελ= υ0-gt=20m/s-10m/s2·5s= -30m/s.
Παράδειγμα 2ο:
Από ύψος Η=60m από το έδαφος εκτοξεύεται για t=0, κατακόρυφα προς τα κάτω, ένα σώμα με αρχική ταχύτητα μέτρου υ0=5m/s. Αν g=10m/s2 και η αντίσταση του αέρα θεωρείται αμελητέα, ζητούνται:
- Η ταχύτητα και η θέση του σώματος τη χρονική στιγμή t1=1s.
- Ποια χρονική στιγμή και με ποια ταχύτητα το σώμα φτάνει στο έδαφος;
Απάντηση:
Στο διπλανό σχήμα έχει σχεδιαστεί ο κατακόρυφος άξονας y΄y πάνω
στον οποίο πραγματοποιείται η κίνηση, με θετική φορά προς τα κάτω και με το σημείο εκτόξευσης Ο στη θέση y=0.
Το σώμα έχει σταθερή επιτάχυνση α= + g, αφού η επιτάχυνση του σώματος έχει φορά προς τα κάτω. Έτσι οι εξισώσεις για την κίνηση του σώματος είναι:
υ= υ0 + α·t → υ=υ0+gt (1) και
Δy= υ0·t + ½ α·t2 → y= υ0·t + ½ g·t2 (2)
1. Αντικαθιστώντας στις παραπάνω σχέσεις t1=1s παίρνουμε:
υ1=υ0+gt= 5+10·1=15m/s και
y1= υ0·t + ½ g·t2 = 5·1+ ½ 10·1=10m.
Πράγμα που σημαίνει ότι το σώμα έχει μετακινηθεί κατά 10m και βρίσκεται σε ύψος h=Η-y=50m από το έδαφος.
2. Τη στιγμή που το σώμα φτάνει στο έδαφος y=60m και με αντικατάσταση στην (2) έχουμε:
y= υ0·t + ½ g·t2 → 60=5t+ ½ 10·t2 ή
5t2 + 5t-60=0 ή
t2 + t – 12=0
οπότε:
άρα ή t=-4s (απορρίπτεται) ή t2=3s (δεκτή λύση)
και υ2= υ0+gt= 5+10·3=35m/s.
Μπορείτε να το κατεβάσετε σε pdf
Ετικέτες
2.1 Ελεύθερη πτώση,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Δευτέρα 14 Δεκεμβρίου 2009
Ελεύθερη πτώση.
Αφήνουμε ένα σώμα να πέσει ελεύθερα και η αντίσταση του αέρα είναι αμελητέα. Τι κίνηση κάνει; Η κίνηση είναι ευθύγραμμη ομαλά μεταβαλλόμενη (επιταχυνόμενη) και, αν όπως γράφει και το σχολικό βιβλίο, στις εξισώσεις της ΕΟΕΚ θέσουμε υ0=0 και α=g παίρνουμε:
υ=υ0+ α·t → υ=g∙t (1)
Δx=υ0∙t + ½ α∙t2 → Δx= ½ g∙t2 (2)
Τι μας δείχνει η εξίσωση (2); Το βιβλίο το ονομάζει διάστημα και το συμβολίζει με s. Είναι διάστημα; Προφανώς ναι, Με την διαφορά ότι το βγάζει από τις εξισώσεις της ευθύγραμμης ομαλά επιταχυνόμενης κίνησης, όπου εκεί οι μαθητές έχουν μάθει να μιλάνε για μετατόπιση. Δεν είναι μετατόπιση αυτή; Και βέβαια είναι. Γιατί λοιπόν μα μην την πούμε απλά μετατόπιση και να την συμβολίσουμε όπως της πρέπει; Πώς; Μα Δy, αφού η κίνηση γίνεται στον άξονα y;
Μήπως έχουμε μάθει το παιδί να δουλεύει στην ευθύγραμμη κίνηση χρησιμοποιώντας τον προσανατολισμένο άξονα x και τώρα θεωρούμε ότι δεν πρέπει να του πούμε, ότι η κίνηση μπορεί να γίνεται και στον κατακόρυφο άξονα y;
Όποιος έχει διδάξει στην Α΄Λυκείου, θα έχει διαπιστώσει ότι πολύ συχνά γίνεται και μπέρδεμα μεταξύ του διαστήματος s και του ύψους h από το οποίο πέφτει το σώμα.
Έτσι πολύ συχνά γράφεται h= ½ g·t2 (3).
Είναι σωστό; Ναι σε κάποια περίπτωση. Αν το σώμα αφεθεί να πέσει από ύψος h από το έδαφος, για την στιγμή που φτάνει στο έδαφος η εξίσωση (3) ισχύει.
Η πρόταση:
Μελετάμε την ελεύθερη πτώση, θεωρώντας μια κίνηση στον κατακόρυφο άξονα y, θέτοντας την προς τα κάτω κατεύθυνση ως θετική και την αρχική θέση, που το σώμα ξεκινά την κίνησή του ως y0=0, με αποτέλεσμα οι εξισώσεις να είναι:
υ=g∙t (1α)
y= ½ g∙t2 (2β)
Εφαρμογή
Ένα σώμα αφήνεται τη χρονική στιγμή t0=0, να πέσει ελεύθερα από ύψος Η=45m από το έδαφος. Αν g=10m/s2 και η αντίσταση του αέρα θεωρηθεί αμελητέα, ζητούνται:
- Να βρεθεί η τιμή της ταχύτητας και το ύψος από το έδαφος τη χρονική στιγμή t1=2s.
- Ποια χρονική στιγμή και με ποια ταχύτητα το σώμα φτάνει στο έδαφος;
- Να γίνουν τα διαγράμματα σε συνάρτηση με το χρόνο:
α) της μετατόπισης του σώματος.
β) της απόστασης του σώματος από το έδαφος (ύψος) .
Απάντηση:
1) Το σώμα αφήνεται να κινηθεί από το σημείο Ο και θα κινηθεί κατακόρυφα στον άξονα y. Θέτουμε για το σημείο Ο, y0=0 και θεωρούμε την προς τα κάτω κατεύθυνση ως θετική. Έτσι μετά από χρονικό διάστημα Δt=t-t0= t το σώμα βρίσκεται στο σημείο Α, στη θέση y και ισχύουν:
υ=g∙t (1α)
y= ½ g∙t2 (2β)
Θέτοντας t1 =2s παίρνουμε:
υ1= 10∙2m/s = 20 m/s και
y1= ½ 10∙22m= 20m
υ=g∙t (1α)
y= ½ g∙t2 (2β)
Θέτοντας t1 =2s παίρνουμε:
υ1= 10∙2m/s = 20 m/s και
y1= ½ 10∙22m= 20m
Το σώμα λοιπόν τη στιγμή t1=2s πέφτει με ταχύτητα 2m/s και απέχει από το έδαφος ύψος h, όπου:
h =Η-y= 45m-20m= 25m.
2) Τη στιγμή που το σώμα φτάνει στο έδαφος y=Η και από την εξίσωση (2 α) παίρνουμε:
Η= ½ g∙t2 →
Έτσι η ταχύτητα πρόσκρουσης του σώματος με το έδαφος είναι:
υ2= gt2= 10·3m/s = 30m/s.
3) Με βάση τα παραπάνω έχουμε ότι η μετατόπιση δίνεται από την σχέση:
y = ½ g∙t2,
ενώ το ύψος από το έδαφος είναι
h=Η-y= Η- ½ g∙t2.
Μπορεί κάποιος να υποστηρίξει ότι πολύ φασαρία για το τίποτα. Θεωρώ ότι τα πράγματα δεν είναι έτσι, αν θέλουμε να πάμε ένα βήμα πιο πέρα και να μελετήσουμε την περίπτωση που το σώμα εκτοξεύεται κατακόρυφα με αρχική ταχύτητα (κατακόρυφη βολή). Αλλά αυτά σε μια νέα ανάρτηση.
Μπορείτε να το κατεβάσετε και σε pdf.
Κατακόρυφη βολή και κάποια συμπεράσματα.
Από το έδαφος εκτοξεύεται για t0=0, κατακόρυφα προς τα άνω, μια μικρή πέτρα με αρχική ταχύτητα υ0=30m/s. Αν g=10m/s2 ενώ η αντίσταση του αέρα είναι αμελητέα, ζητούνται:
- Ο χρόνος ανόδου και το μέγιστο ύψος που θα φτάσει η πέτρα.
- Ποιες χρονικές στιγμές η πέτρα βρίσκεται σε ύψος h=40m; Ποια η ταχύτητα της πέτρας στο ύψος αυτό;
- Ποια χρονική στιγμή και με ποια ταχύτητα η πέτρα επιστρέφει στο έδαφος;
Ετικέτες
2.1 Ελεύθερη πτώση,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Δευτέρα 7 Δεκεμβρίου 2009
Ισορροπία δύο σωμάτων.
Δύο σώματα Α και Γ με μάζες 3kg και 1kg αντίστοιχα, κρέμονται με αβαρή νήματα όπως στο σχήμα. Αν g=10m/s2:
Α. Ποιες προτάσεις είναι σωστές και ποιες λάθος:
- Το σώμα Α δέχεται δύο δυνάμεις. Την έλξη της Γης, που είναι 30Ν και την αντίδρασή της προς τα πάνω επίσης μέτρου 30Ν.
- Το σώμα Γ δέχεται τρεις δυνάμεις. Το βάρος του, το βάρος του σώματος Α και την τάση του πάνω νήματος.
- Η τάση του νήματος που συνδέει τα δύο σώματα έχει μέτρο 30Ν.
- Η τάση του πάνω νήματος είναι ίση με 10Ν.
Β. Σε μια στιγμή κόβουμε το πάνω νήμα και το σύστημα πέφτει ελεύθερα. Αν αγνοήσουμε την αντίσταση του αέρα, τότε η τάση του νήματος που συνδέει τα δύο σώματα στην διάρκεια της πτώσης είναι:
- μηδέν.
- ίση με το βάρος της σφαίρας Α.
- ίση με την διαφορά των δύο βαρών.
- ίση με το άθροισμα των βαρών των δύο σωμάτων.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Τι δεν μπορεί να συμβεί.
Ένα σώμα δέχεται δύο δυνάμεις με ίσα μέτρα όπως στο σχήμα.
Τι από τα παρακάτω δεν μπορεί να συμβεί;
- Το σώμα παραμένει ακίνητο.
- Το σώμα επιταχύνεται προς τα δεξιά.
- Το σώμα κινείται προς τα αριστερά με σταθερή ταχύτητα.
- Το σώμα κινείται στη διεύθυνση του άξονα y με σταθερή ταχύτητα.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Κυριακή 6 Δεκεμβρίου 2009
Δράση-Αντίδραση και επιτάχυνση.
Ένα σώμα Σ μάζας 4kg αφήνεται στο πάνω ελεύθερο άκρο ενός κατακόρυφου ελατηρίου σταθεράς k=200Ν/m, το άλλο του οποίου στηρίζεται στο έδαφος. Το σώμα αρχίζει και συσπειρώνει το ελατήριο.
Για τη θέση που το σώμα έχει επιτάχυνση α=4m/s2, με φορά προς τα κάτω, η δύναμη που δέχεται το ελατήριο από το σώμα είναι:
i) Το βάρος του σώματος Σ.
ii) Μια δύναμη ίση με το βάρος του σώματος.
iii) Δύναμη μεγαλύτερη από το βάρος του Σ.
iv) Δύναμη μικρότερη από το βάρος του Σ.
v) Δύναμη με φορά προς τα πάνω και μέτρο 24Ν.
vi) Δύναμη με φορά προς τα κάτω και μέτρο 24Ν.
Ποιες από τις παραπάνω προτάσεις είναι σωστές;
Δίνεται g=10m/s2.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Δύναμη και μεταβολή της ταχύτητας.
Ένα σώμα κινείται σε λείο οριζόντιο επίπεδο και στο διάγραμμα δίνεται η ταχύτητα του σώματος σε συνάρτηση με το χρόνο.
Ποιο από τα παρακάτω σχήματα που δείχνουν την ταχύτητα και τη συνισταμένη δύναμη, είναι σωστό για τις χρονικές στιγμές:
i) t1= 1s
ii) t2=3s
iii) t3=5s
Να εξηγείστε γιατί απορρίπτονται τα άλλα σχήματα.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Τριβή και 3ος Νόμος του Νεύτωνα.
Πάνω σε ένα τραπέζι ηρεμεί ένα κιβώτιο μάζας 0,5kg. Ασκούμε πάνω του, μέσω ενός δυναμομέτρου δύναμη μέτρου 1Ν και το κιβώτιο δεν μετακινείται.
1) Να σχεδιάστε τις δυνάμεις που ασκούνται στο κιβώτιο και να υπολογίστε τα μέτρα τους.
2) Το κιβώτιο ασκεί στο τραπέζι:
i. Το βάρος του.
ii. Δύναμη κατακόρυφη ίση κατά μέτρο με το βάρος του.
iii. Πλάγια δύναμη μέτρου μεγαλύτερη του βάρους του.
Να δικαιολογήστε την απάντησή σας.
3) Τραβώντας με μεγαλύτερη δύναμη F1=2Ν, μετακινούμε το κιβώτιο κατά 50cm σε 1s. Να υπολογιστεί το μέτρο της τριβής ολίσθησης μεταξύ κιβωτίου και τραπεζιού.
Δίνεται g=10m/s2.
Σάββατο 5 Δεκεμβρίου 2009
Αδράνεια σώματος και θεμελιώδης νόμος.
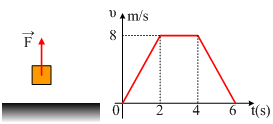
Ένα σώμα ηρεμεί στο έδαφος. Δένουμε το σώμα με ένα νήμα ασκώντας πάνω του μια κατακόρυφη δύναμη F, με αποτέλεσμα το σώμα να αρχίζει προς τα πάνω και στο διάγραμμα δίνεται πως μεταβάλλεται η ταχύτητά του σε συνάρτηση με το χρόνο.
Αν το μέτρο της δύναμης από 0-2s είναι F=42Ν, ζητούνται:
i) Η μάζα του σώματος.
ii) Πότε έχει μεγαλύτερη αδράνεια το σώμα τη στιγμή t1=1s ή τη στιγμή t2=3s;
iii) Να κάνετε το διάγραμμα του μέτρου της ασκούμενης δύναμης F σε συνάρτηση με το χρόνο.
iv) Πόσο απέχει το σώμα από το έδαφος τη στιγμή t3=6s;
Δίνεται g=10m/s2.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Τετάρτη 2 Δεκεμβρίου 2009
Συνολική κίνηση με τριβές.
Ένα σώμα μάζας 2kg ηρεμεί σε οριζόντιο επίπεδο στη θέση Α. Για t=0 ασκούμε πάνω του μια σταθερή οριζόντια δύναμη F=10Ν, μέχρι τη στιγμή t1=3s, όπου η δύναμη καταργείται, ενώ το σώμα έχει ταχύτητα υ1=6m/s.
i) Ποια επιτάχυνση είχε το σώμα για όσο χρόνο ασκείτο η δύναμη F;
ii) Σε απόσταση από τη θέση Α θα σταματήσει τελικά το σώμα;
Ετικέτες
2. Δυναμική,
9. Επίπεδο 2.,
Λάμπρος Θεοδώρου
Τρίτη 1 Δεκεμβρίου 2009
Πόση θα γίνει η απόσταση των σωμάτων;
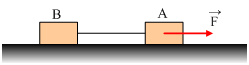
Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m1=m2=2kg και ηρεμούν σε λείο οριζόντιο, δεμένα στα άκρα νήματος μήκους L=2m. Για t=0 ασκούμε στο Α σταθερή οριζόντια δύναμη μέτρου F=12Ν.
Τη χρονική στιγμή t1=3s το νήμα που συνδέει τα δύο σώματα κόβεται ενώ η δύναμη F συνεχίζει να ασκείται στο σώμα Α.
i) Ποια η ταχύτητα των δύο σωμάτων τη στιγμή t1;
ii) Πόσο απέχουν τα δύο σώματα τη χρονική στιγμή t2=5s;
Δίνεται g=10m/s2.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
1ος Νόμος του Νεύτωνα. Μια ερώτηση.
Το σώμα Α του σχήματος είναι ακίνητο, ενώ το Β κινείται με σταθερή ταχύτητα →υ .
Σε ποιο από τα δύο σώματα η συνισταμένη δύναμη είναι μεγαλύτερη;
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Σάββατο 28 Νοεμβρίου 2009
Όταν η επιτάχυνση α δεν είναι ανάλογη της δύναμης F, λόγω της τριβής.
Ένα κομμάτι ξύλου με μάζα 2 Kg βρίσκεται σε οριζόντιο επίπεδο.
Εξασκώντας στο ξύλινο αντικείμενο οριζόντια δύναμη F, διαπιστώνουμε ότι όταν F=8N τότε μόλις αρχίζει να κινείται με ασήμαντη σταθερή ταχύτητα.

1) Με πόση επιτάχυνση θα κινηθεί, όταν F=20N και όταν F = 32N;
2) Να παρασταθεί γραφικά η επιτάχυνση (α) σε συνάρτηση της δύναμης F.
Εκφώνηση και λύση <ΕΔΩ πατώντας>
Ετικέτες
2. Δυναμική,
3.1.Τριβή,
ΜιλτοΣ
Τετάρτη 25 Νοεμβρίου 2009
Διαγώνισμα Φυσικής. Κινηματική.
Ένα αυτοκίνητο κινείται ευθύγραμμα σε δρόμο που ταυτίζουμε με τον άξονα x και τη χρονική στιγμή t=0 περνά από σημείο Α με xΑ=10m και κινείται προς τα δεξιά (θετική κατεύθυνση) με ταχύτητα μέτρου 8m/s ενώ φρενάρει αποκτώντας σταθερή επιτάχυνση, με φορά προς τ’ αριστερά και μέτρο 2m/s2.
i) Ποια χρονική στιγμή t1 θα σταματήσει το αυτοκίνητο;
ii) Ποια η μετατόπισή του και ποια η θέση του τη στιγμή t1;
iii) Να κάνετε το διάγραμμα της θέσης του αυτοκινήτου σε συνάρτηση με το χρόνο μέχρι τη χρονική στιγμή t= 6s, σε βαθμολογημένους άξονες.
Ετικέτες
1. Κινηματική,
8. Τest,
Διονύσης Μάργαρης
Κυριακή 22 Νοεμβρίου 2009
Μερικοί μύθοι για την ΤΡΙΒΗ
Με αφορμή αντίστοιχη ανάρτηση του Διονύση έγραψα αυτό το αρχείο και το έδωσα σε ορισμένους μαθητές της Β΄ Λυκείου που ενδιαφέρονται να μάθουν κάτι παραπάνω από τους γνωστούς και εύπεπτους "τύπους".
Πρώτος μύθος:
Η τριβή έχει ΠΑΝΤΑ τέτοια φορά ώστε ν’ αντιστέκεται στην κίνηση!!!.
Δεύτερος μύθος:
Το έργο της τριβής ολίσθησης είναι ΠΑΝΤΑ ΑΡΝΗΤΙΚΟ!!! και μετράει την ενέργεια που μετατρέπεται σε θερμική, ενώ το έργο της στατικής τριβής είναι ΠΑΝΤΑ ΜΗΔΕΝΙΚΟ!!!.
Η αλήθεια...
Πρώτος μύθος:
Η τριβή έχει ΠΑΝΤΑ τέτοια φορά ώστε ν’ αντιστέκεται στην κίνηση!!!.
Δεύτερος μύθος:
Το έργο της τριβής ολίσθησης είναι ΠΑΝΤΑ ΑΡΝΗΤΙΚΟ!!! και μετράει την ενέργεια που μετατρέπεται σε θερμική, ενώ το έργο της στατικής τριβής είναι ΠΑΝΤΑ ΜΗΔΕΝΙΚΟ!!!.
Η αλήθεια...
Ετικέτες
2. Δυναμική,
6. Έργο-Ενέργεια,
9. Επίπεδο 3.,
Νίκος Ανδρεάδης
Πέμπτη 19 Νοεμβρίου 2009
Θεμελιώδης νόμος της δυναμικής.
Ένα σώμα μάζας m=2kg ηρεμεί σε ένα λείο οριζόντιο επίπεδο. Σε μια στιγμή t=0 δέχεται την επίδραση δύο οριζοντίων δυνάμεων με μέτρα F1=10Ν και F2=6Ν, όπως στο σχήμα.
Τη χρονική στιγμή t1 παύει να ασκείται η δύναμη F1, οπότε τη χρονική στιγμή t2=10s η ταχύτητα του σώματος μηδενίζεται στιγμιαία.
1) Ποιες προτάσεις είναι σωστές και ποιες λάθος.
Α) Από 0-t1 το σώμα αποκτά σταθερή επιτάχυνση προς τα δεξιά.
Β) Μόλις πάψει να ασκείται η δύναμη F1 το σώμα θα κινηθεί αμέσως προς τα αριστερά.
Γ) Από t1 έως t2 το σώμα εκτελεί ευθύγραμμη ομαλή κίνηση.
Δ) Το σώμα παρουσιάζει μεγαλύτερη αδράνεια στο χρονικό διάστημα από t1 έως t2.
2) Ποια χρονική στιγμή t1 παύει να ασκείται η δύναμη F1;
3) Να βρεθεί η μέγιστη ταχύτητα που αποκτά το σώμα στο παραπάνω χρονικό διάστημα;
Ετικέτες
2. Δυναμική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Ένα θέμα του διαγωνισμού Φυσικής της Ε.Ε.Φ. του 2008
Το σύστημα του παρακάτω σχήματος είναι σε ισορροπία. Το δυναμόμετρο θα δείχνει:
| α.100Ν | β. 50Ν | γ. 0Ν | δ. 25Ν |
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Συνολική (συνισταμένη) Δύναμη.
Σε ποιες από τις παρακάτω περιπτώσεις ασκείται συνολική δύναμη στο σώμα.
- Το σώμα αφήνεται από ύψος h=1m.
- Ένα σώμα ηρεμεί πάνω στο τραπέζι.
- Ένα αυτοκίνητο κινείται σε ευθύγραμμο δρόμο με σταθερή ταχύτητα.
- Ένα αυτοκίνητο παίρνει μια στροφή με ταχύτητα σταθερού μέτρου 50km/h.
- Ένα λάστιχο είναι τεντωμένο.
- Στο στρώμα, όταν πάνω του ξαπλώσει ένας άνθρωπος.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 1.,
Διονύσης Μάργαρης
Εγγραφή σε:
Αναρτήσεις (Atom)