Τετάρτη 30 Οκτωβρίου 2013
Δύο μεταβαλλόμενες κινήσεις.
Παρασκευή 25 Οκτωβρίου 2013
ΔΙΑΔΟΧΙΚΕΣ ΚΙΝΗΣΕΙΣ ΚΙΝΗΤΟΥ
 Αυτοκίνητο κινείται την χρονική στιγμή t0
= 0, ευθύγραμμα με σταθερή ταχύτητα μέτρου υ1 = 10 m/s
ως την χρονική στιγμή t1
= 10 s, στη συνέχεια επιταχύνεται με σταθερή επιτάχυνση μέτρου α2 = 2
m/s2
μέχρι την χρονική στιγμή t2
= 30 s
και τέλος επιβραδύνεται με σταθερή επιβράδυνση μέτρου α3 = 5 m/s2
μέχρι την χρονική στιγμή t3
που σταματά.
Αυτοκίνητο κινείται την χρονική στιγμή t0
= 0, ευθύγραμμα με σταθερή ταχύτητα μέτρου υ1 = 10 m/s
ως την χρονική στιγμή t1
= 10 s, στη συνέχεια επιταχύνεται με σταθερή επιτάχυνση μέτρου α2 = 2
m/s2
μέχρι την χρονική στιγμή t2
= 30 s
και τέλος επιβραδύνεται με σταθερή επιβράδυνση μέτρου α3 = 5 m/s2
μέχρι την χρονική στιγμή t3
που σταματά. Τετάρτη 23 Οκτωβρίου 2013
ΚΙΝΗΣΗ ΜΕ ΧΡΟΝΙΚΗ ΚΑΘΥΣΤΕΡΗΣΗ
 Στο διπλανό διάγραμμα βλέπουμε τις γραφικές παραστάσεις των ταχυτήτων δύο κινητών Α και Β. Οι αρχικές θέσεις είναι x01 = 5
m και x02 = 1 m, αντίστοιχα.
Στο διπλανό διάγραμμα βλέπουμε τις γραφικές παραστάσεις των ταχυτήτων δύο κινητών Α και Β. Οι αρχικές θέσεις είναι x01 = 5
m και x02 = 1 m, αντίστοιχα. Ανακρίνοντας τρία διαγράμματα…
α) Μηδέν, β) Θετική, γ) Αρνητική.
α) Μηδέν, β) Θετική, γ) Αρνητική.
α) Μέγιστη, β) Μηδέν, γ) Θετική.
α) Μία φορά, β) Δύο φορές, γ) Τρεις φορές.
Πέμπτη 17 Οκτωβρίου 2013
ΤΟ ΠΡΩΙΝΟ ΤΟΥ ΔΙΟΝΥΣΗ
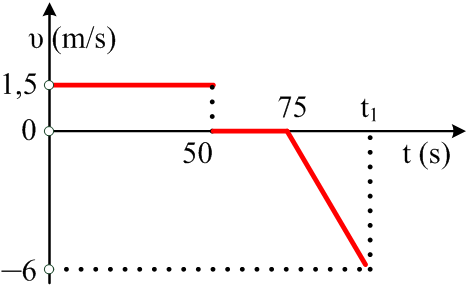 Ο
κύριος Διονύσης που έχει βγει στην σύνταξη, σηκώνεται κάθε πρωί να πιει το
καφεδάκι του και μετά πάει στο περίπτερο να αγοράσει την εφημερίδα του. Μιλάει
λίγο με τον περιπτερά και εκείνη τη στιγμή αρχίζει να βρέχει οπότε επιστρέφει
σπίτι του επιταχυνόμενος. Στο διπλανό διάγραμμα φαίνεται η ταχύτητα του Διονύση
σε συνάρτηση με το χρόνο, από την στιγμή που έφυγε από το σπίτι του έως την
επιστροφή του σ’ αυτό.
Ο
κύριος Διονύσης που έχει βγει στην σύνταξη, σηκώνεται κάθε πρωί να πιει το
καφεδάκι του και μετά πάει στο περίπτερο να αγοράσει την εφημερίδα του. Μιλάει
λίγο με τον περιπτερά και εκείνη τη στιγμή αρχίζει να βρέχει οπότε επιστρέφει
σπίτι του επιταχυνόμενος. Στο διπλανό διάγραμμα φαίνεται η ταχύτητα του Διονύση
σε συνάρτηση με το χρόνο, από την στιγμή που έφυγε από το σπίτι του έως την
επιστροφή του σ’ αυτό.Τετάρτη 16 Οκτωβρίου 2013
Επιλέξτε το σωστό διάγραμμα.
Τρίτη 15 Οκτωβρίου 2013
Η κίνηση και τα διαγράμματα θέσεις.
Δευτέρα 14 Οκτωβρίου 2013
Μελετώντας τις κινήσεις τριών σωμάτων.
Παρασκευή 11 Οκτωβρίου 2013
Δυο παιδιά περπατούν...
Η ΑΣΚΗΣΗ 5 ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΜΕ ΠΡΟΕΚΤΑΣΕΙΣ
 Περιπολικό αρχίζει να καταδιώκει μοτοσικλετιστή που βρίσκεται σε απόσταση d = 500 m μπροστά από το περιπολικό. Το περιπολικό έχει σταθερή ταχύτητα υπ
= 30 m/s, ενώ ο μοτοσικλετιστής κινείται με σταθερή ταχύτητα υΜ = 20 m/s. Να βρεθούν:
Περιπολικό αρχίζει να καταδιώκει μοτοσικλετιστή που βρίσκεται σε απόσταση d = 500 m μπροστά από το περιπολικό. Το περιπολικό έχει σταθερή ταχύτητα υπ
= 30 m/s, ενώ ο μοτοσικλετιστής κινείται με σταθερή ταχύτητα υΜ = 20 m/s. Να βρεθούν:
α. O χρόνος t που απαιτείται για να φτάσει το περιπολικό τον μοτοσικλετιστή.
β. Το διάστημα που θα διανύσει το περιπολικό στο χρόνο αυτό.
γ. Να γίνουν τα διαγράμματα ταχύτητας χρόνου, διαστήματος χρόνου, μετατόπισης χρόνου και θέσης χρόνου και για τα δύο κινητά σε κοινά συστήματα αξόνων, θεωρώντας ότι το σημείο Α βρίσκεται στην αρχή των αξόνων.
δ. Όταν ο μοτοσικλετιστής βρίσκεται στο μέσο, μεταξύ της αφετηρίας του και του σημείου συνάντησης πόσο απέχει από το περιπολικό;
Πέμπτη 10 Οκτωβρίου 2013
«Αποκαλυπτικά διαγράμματα ταχύτητας – χρόνου»
«Αποκαλυπτικά διαγράμματα ταχύτητας – χρόνου»
ΠΕΡΑΣΜΑ ΓΕΦΥΡΑΣ ΜΕ ΝΤΑΛΙΚΑ
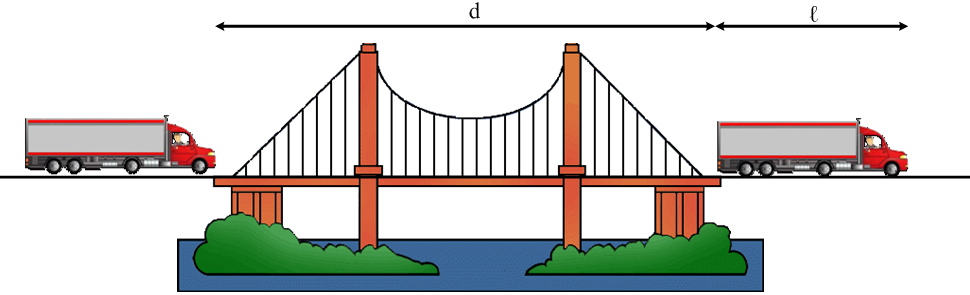 Μια νταλίκα έχει μήκος ℓ = 10 m,
κινείται με ταχύτητα υ = 10m/s και περνά μια γέφυρα μήκους d
= 1490 m. Να βρείτε:
Μια νταλίκα έχει μήκος ℓ = 10 m,
κινείται με ταχύτητα υ = 10m/s και περνά μια γέφυρα μήκους d
= 1490 m. Να βρείτε:Τρίτη 8 Οκτωβρίου 2013
Δύναμη F-Τριβή Ολίσθησης
Η κίνηση και οι παρατηρητές.
Τετάρτη 2 Οκτωβρίου 2013
Άσκηση. Νόμοι Νεύτωνα.
Μια μπάλα κινείται.
Τρίτη 1 Οκτωβρίου 2013
Ένα ρεκόρ του Γιάννη…
Η ΑΣΚΗΣΗ 4 ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΜΕ ΠΡΟΕΚΤΑΣΕΙΣ
 Δύο αυτοκίνητα ξεκινάνε ταυτόχρονα
από τα σημεία A και B μιας ευθύγραμμης διαδρομής κινούμενα αντίθετα με σταθερές
ταχύτητες υ1 = 36 km/h και υ2 = 54 km/h αντίστοιχα.
Δύο αυτοκίνητα ξεκινάνε ταυτόχρονα
από τα σημεία A και B μιας ευθύγραμμης διαδρομής κινούμενα αντίθετα με σταθερές
ταχύτητες υ1 = 36 km/h και υ2 = 54 km/h αντίστοιχα.
α. Να βρεθεί μετά από πόσο χρόνο και σε ποιο σημείο θα συναντηθούν τα αυτοκίνητα, αν είναι AB = 1 km.
β. Να γίνουν τα διαγράμματα ταχύτητας χρόνου και διαστήματος χρόνου και για τα δύο κινητά σε κοινά συστήματα αξόνων.
γ. Να γίνουν τα διαγράμματα μετατόπισης χρόνου και θέσης χρόνου, για τα δύο κινητά σε κοινά συστήματα αξόνων, θεωρώντας ότι το σημείο Α βρίσκεται στην αρχή των αξόνων















