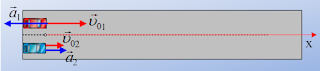
Σώμα Σ1
εκτοξεύεται κατακόρυφα από σημείο Α του εδάφους τη χρονική στιγμή to = 0, με αρχική ταχύτητα
μέτρου υο =10 m/s. Την ίδια στιγμή, από σημείο Β της
κατακόρυφης που περνάει από το Α, αφήνεται να πέσει ελεύθερα δεύτερο σώμα Σ2.
Η απόσταση ΑΒ είναι Η = 80 m.
1) Να
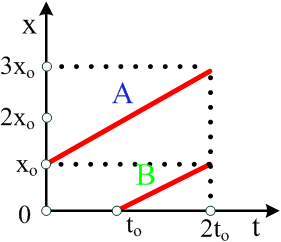
γράψετε τις χρονικές εξισώσεις θέσης των δύο σωμάτων, χρησιμοποιώντας ως αρχή
του y άξονα το σημείο Α και θετική φορά την προς τα επάνω.
2) Ποιά
χρονική στιγμή θα επιστρέψει στο έδαφος το Σ1 και σε ποιο μέγιστο
ύψος θα φτάσει;
3) Να
εξετάσετε αν τα δύο σώματα θα συναντηθούν προτού να πέσουν στο έδαφος.
4) Αν όχι,
να βρείτε το ελάχιστο μέτρο της αρχικής ταχύτητας υο ώστε να γίνει η συνάντηση.
5) Αν η
αρχική ταχύτητα του Σ1 έχει τώρα μέτρο υοʹ = 40 m/s, ποιά είναι
η νέα εξίσωση θέσης του και σε ποιό ύψος θα συναντηθούν;
6) Να
απεικονίσετε σε συνάρτηση με το χρόνο σε κοινό διάγραμμα τις εξισώσεις κίνησης
των δύο σωμάτων στις περιπτώσεις των ερωτημάτων (1) και (5).
(Δίνεται: g = 10 m/s²)
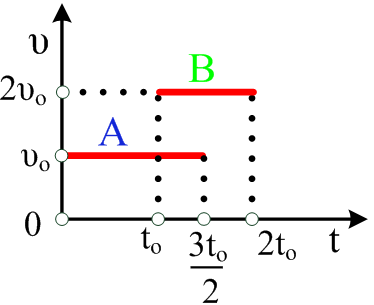
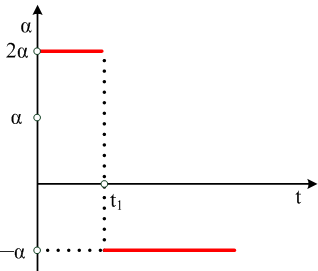 Ένα κινητό την χρονική στιγμή t0
= 0 βρίσκεται ακίνητο στην αρχή των αξόνων. Η γραφική παράσταση της επιτάχυνσης με το χρόνο φαίνεται στο σχήμα.
Ένα κινητό την χρονική στιγμή t0
= 0 βρίσκεται ακίνητο στην αρχή των αξόνων. Η γραφική παράσταση της επιτάχυνσης με το χρόνο φαίνεται στο σχήμα.


 1.
1.