Σάββατο 26 Δεκεμβρίου 2015
Πέμπτη 24 Δεκεμβρίου 2015
Μια κατακόρυφη κίνηση πριν και μετά το κόψιμο του νήματος.
Ένα σώμα μάζας 0,5kg ηρεμεί στο
έδαφος. Τη στιγμή t=0, δέχεται μέσω νήματος μια κατακόρυφη σταθερή δύναμη μέτρου
F=9Ν, μέχρι τη στιγμή t1=2s, όπου το νήμα σπάει και το σώμα κινείται
πια «ελεύθερα». Αντίσταση του αέρα δεν υπάρχει ενώ g=10m/s2.
i) Να υπολογίστε την επιτάχυνση του σώματος για το
χρονικό διάστημα που στο σώμα ασκείται η δύναμη F.
ii) Πόσο απέχει το σώμα από το έδαφος τη στιγμή που
σπάει το νήμα;
iii) Ποια χρονική στιγμή το σώμα σταματά την ανοδική
του κίνηση; Σε ποιο ύψος βρίσκεται τη στιγμή αυτή;
iv) Να βρεθεί η χρονική στιγμή που το σώμα επιστρέφει
στο έδαφος. Ποια η ταχύτητά του τη στιγμή αυτή;
v) Να γίνουν τα διαγράμματα σε συνάρτηση με το χρόνο:
α) της
ταχύτητας του σώματος, β) της απόστασής
του από το έδαφος.
Κυριακή 20 Δεκεμβρίου 2015
Επιταχυνόμενες κινήσεις σε αντίθετες κατευθύνσεις.
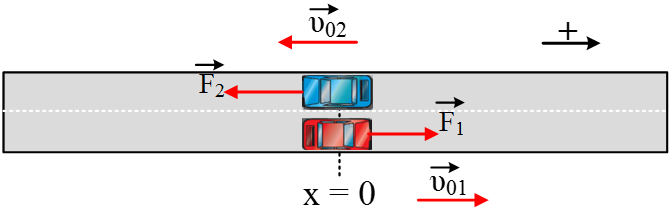 Δύο αυτοκινητάκια Α1 και Α2 με μάζες
m1
= 3 kg
και m2
= 2 kg
περνούν την χρονική στιγμή t0
= 0 από το ίδιο σημείο του δρόμου που το θεωρούμε ως
x0
= 0, κινούμενα αντίθετα όπως στο σχήμα, με ταχύτητες μέτρου υ01 = 10
m/s
και υ02 = 4
m/s.
Την ίδια χρονική στιγμή (t0
= 0) ασκούνται στα δύο αυτοκινητάκια δυνάμεις ίδιου μέτρου
F = 12
N
και αντίθετης φοράς ομόρροπες με την κίνηση τους.
Δύο αυτοκινητάκια Α1 και Α2 με μάζες
m1
= 3 kg
και m2
= 2 kg
περνούν την χρονική στιγμή t0
= 0 από το ίδιο σημείο του δρόμου που το θεωρούμε ως
x0
= 0, κινούμενα αντίθετα όπως στο σχήμα, με ταχύτητες μέτρου υ01 = 10
m/s
και υ02 = 4
m/s.
Την ίδια χρονική στιγμή (t0
= 0) ασκούνται στα δύο αυτοκινητάκια δυνάμεις ίδιου μέτρου
F = 12
N
και αντίθετης φοράς ομόρροπες με την κίνηση τους.
α. να βρείτε
τις επιταχύνσεις που αποκτούν τα δύο αυτοκινητάκια
β. να γράψετε
τις εξισώσεις της κίνησης τους
γ. να γράψετε
την εξίσωση που περιγράφει την απόσταση τους κάθε χρονική στιγμή και από εκεί να
υπολογίσετε ποια χρονική στιγμή η απόσταση τους θα είναι
d =
195 m
δ. να γράψετε
την εξίσωση της ταχύτητας για κάθε αυτοκινητάκι και να προσδιορίσετε ποια
χρονική στιγμή τα μέτρα των ταχυτήτων τους θα είναι ίσα
ε. να γίνουν τα
διαγράμματα ταχύτητας χρόνου και θέσης χρόνου για τα δύο αυτοκινητάκια ως την
στιγμή t3
= 5s
στ.
αν την χρονική στιγμή
t0
= 0 οι δυνάμεις που δέχονται τα δύο αυτοκινητάκια ήταν αντίθετες κατεύθυνσης απ’
αυτές που είναι στο σχήμα πόσο διάστημα διανύει το ένα αυτοκινητάκι από την
στιγμή που το άλλο ηρεμεί και μετά;
Πατήστε την εικόνα για την λύση.
Ετικέτες
2. Δυναμική,
Βασίλης Δουκατζής
Σάββατο 19 Δεκεμβρίου 2015
Ακινησία και κίνηση ενός σώματος στο άκρο ελατηρίου.
Το αμαξίδιο του σχήματος ηρεμεί
σε οριζόντιο επίπεδο. Το ιδανικό ελατήριο κρέμεται, δεμένο στο ένα του άκρο, έχοντας
μήκος l0=40cm. Δένουμε στο κάτω άκρο του ένα σώμα Σ1 βάρους
20Ν και το αφήνουμε να ηρεμήσει, οπότε το ελατήριο αποκτά μήκος l1=50cm.
i) Να σχεδιάστε τις δυνάμεις που ασκούνται στο σώμα και να υπολογίστε
τη σταθερά του ελατηρίου.
Σε επανάληψη του πειράματος, το
αμαξίδιο κινείται προς τα δεξιά με σταθερή ταχύτητα υ1=2m/s, ενώ στο
άκρο του ελατηρίου είναι δεμένο ένα δεύτερο σώμα Σ2 βάρους 60Ν, το οποίο
στηρίζεται και στο αμαξίδιο, ενώ το μήκος του ελατηρίου είναι l2=60cm.
ii) Να υπολογίστε
τη δύναμη που ασκεί το σώμα Σ2 στο ελατήριο.
iii) Το σώμα Σ2 δέχεται κάποια δύναμη από
το αμαξίδιο, έστω F1. Αυτή είναι κατακόρυφη ή όχι και γιατί; Να υπολογιστεί
το μέτρο της δύναμης F1.
iv) Σε μια
στιγμή το αμαξίδιο αρχίζει να επιταχύνεται προς τα δεξιά, αυξάνοντας την ταχύτητά
του, χωρίς να γλιστράει πάνω του το σώμα Σ2. Στη διάρκεια της επιτάχυνσης
του αμαξιδίου, το αμαξίδιο ασκεί στο σώμα Σ2 δύναμη:
α) Κατακόρυφη με μέτρο F3=F1.
β) Οριζόντια με κατεύθυνση προς τα δεξιά και μέτρο F3>F1.
γ) Τίποτα από τα παραπάνω.
Δευτέρα 14 Δεκεμβρίου 2015
Ένα εκκρεμές πάνω σε φορτηγό.
Ένα φορτηγάκι κινείται ευθύγραμμα
σε οριζόντιο δρόμο και στο παρακάτω διάγραμμα δίνεται η ταχύτητά του σε συνάρτηση
με το χρόνο.
Πάνω στο φορτηγό έχει στερεωθεί
κατάλληλα ένα στήριγμα, από το οποίο κρέμεται μέσω νήματος ένα σώμα Σ. Στο
παρακάτω σχήμα δείχνει τρεις διαφορετικές θέσεις του νήματος κατά την κίνηση
του φορτηγού, όπου η γωνία που σχηματίζει το
νήμα με την κατακόρυφη διεύθυνση παραμένει σταθερή.
Με βάση το διάγραμμα της ταχύτητας να συμπληρώσετε τον
παρακάτω πίνακα, αντιστοιχώντας τα χρονικά διαστήματα κίνησης με την εικόνα που
δείχνει τη σωστή σχέση του νήματος,
δίνοντας και σύντομες επεξηγήσεις.
Κυριακή 6 Δεκεμβρίου 2015
Ποια στιγμή να καταργήσω την δύναμη;
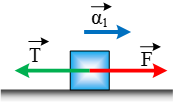 Μικρό
σώμα μάζας
m
= 5 kg βρίσκεται αρχικά ακίνητο σε
οριζόντιο επίπεδο. Η τριβή ολίσθησης μεταξύ του σώματος και του οριζόντιου
επιπέδου έχει μέτρο 20 Ν. Τη χρονική στιγμή t0
= 0 s ασκείται στο σώμα σταθερή οριζόντια δύναμη
F μέτρου ίσο με 50 Ν με
την επίδραση της οποίας το σώμα αρχίζει να κινείται στο οριζόντιο επίπεδο.
Δίνεται ότι η επίδραση του αέρα είναι αμελητέα και η επιτάχυνση της βαρύτητας
είναι
g
= 10 m/ s2.
Να υπολογίσετε:
Μικρό
σώμα μάζας
m
= 5 kg βρίσκεται αρχικά ακίνητο σε
οριζόντιο επίπεδο. Η τριβή ολίσθησης μεταξύ του σώματος και του οριζόντιου
επιπέδου έχει μέτρο 20 Ν. Τη χρονική στιγμή t0
= 0 s ασκείται στο σώμα σταθερή οριζόντια δύναμη
F μέτρου ίσο με 50 Ν με
την επίδραση της οποίας το σώμα αρχίζει να κινείται στο οριζόντιο επίπεδο.
Δίνεται ότι η επίδραση του αέρα είναι αμελητέα και η επιτάχυνση της βαρύτητας
είναι
g
= 10 m/ s2.
Να υπολογίσετε:
α.
το μέτρο της επιτάχυνσης με την οποία κινείται το σώμα,
β.
το ρυθμό μεταβολής της θέσης την χρονική στιγμή
t1
= 2 s,
γ. την χρονική στιγμή t2
που πρέπει να καταργήσουμε την δύναμη F ώστε το σώμα
να σταματήσει την χρονική στιγμή t3
= 15 s
δ. την μέγιστη ταχύτητα κατά την διάρκεια
της κίνησης και την συνολική μετατόπιση.
Πατήστε την εικόνα για την λύση.
Ετικέτες
2. Δυναμική,
Βασίλης Δουκατζής
Εγγραφή σε:
Αναρτήσεις (Atom)









