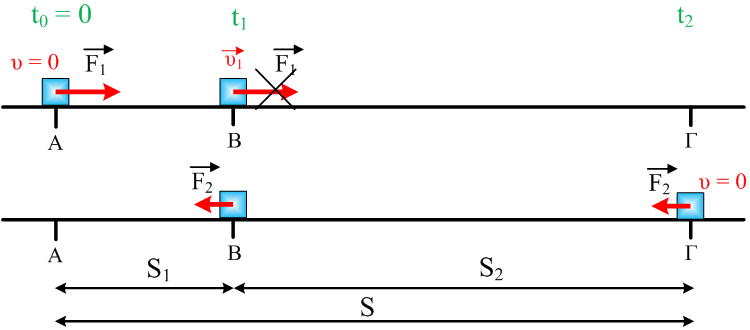
Στο σχήμα δίνονται δυο σώματα Α και Σ που ηρεμούν σε
οριζόντιο επίπεδο. Τη στιγμή t0=0 ασκείται στο κάτω σώμα Α μια
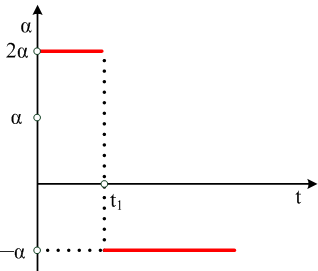
οριζόντια δύναμη F, το μέτρο της οποίας μεταβάλλεται όπως στο διπλανό
διάγραμμα. Δίνονται οι μάζες των δύο σωμάτων Α και Σ, Μ=4kg και m=1kg
αντίστοιχα, ενώ οι συντελεστές τριβής τόσο μεταξύ των δύο σωμάτων, όσο και
μεταξύ του Α και του εδάφους είναι μ=μs=0,2, ενώ g=10m/s2.
i)
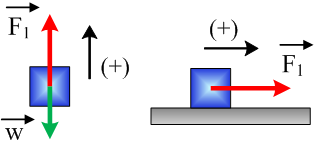
Για τη χρονική στιγμή t1=5s, αφού σχεδιάστε τις δυνάμεις που ασκούνται
σε κάθε σώμα, να χαρακτηρίστε ως σωστές ή λανθασμένες τις προτάσεις:
Α)
Το σώμα Α δέχεται δύναμη τριβής με φορά
προς τα αριστερά μέτρου 5Ν.
Β)
Το σώμα Σ δέχεται δύναμη τριβής προς τα αριστερά.
ii)
Για τη χρονική στιγμή t2=15s (όπου F=15Ν), να σχεδιάστε ξανά τις δυνάμεις
που ασκούνται στα σώματα και να υπολογίστε τα μέτρα τους.
iii)
Να βρείτε ξανά τις δυνάμεις που ασκούνται στα σώματα τη χρονική t3=25s.
ή




 1.
1.

 Σώμα μάζας m = 5
Σώμα μάζας m = 5 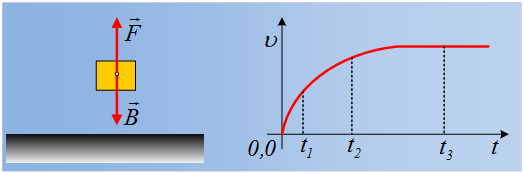



 1.
1.
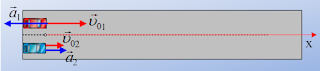





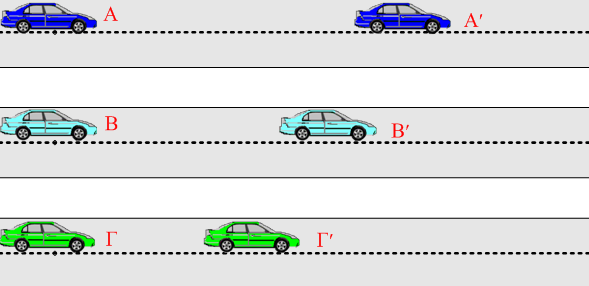
 Αυτοκίνητο κινείται την χρονική στιγμή
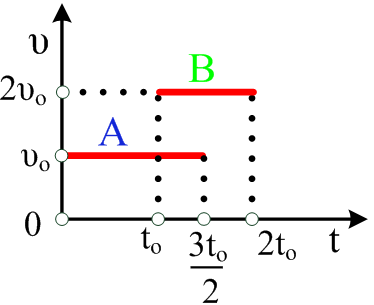
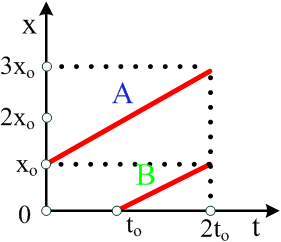
Αυτοκίνητο κινείται την χρονική στιγμή  Στο διπλανό διάγραμμα βλέπουμε τις γραφικές παραστάσεις των ταχυτήτων δύο κινητών Α και Β. Οι αρχικές θέσεις είναι
Στο διπλανό διάγραμμα βλέπουμε τις γραφικές παραστάσεις των ταχυτήτων δύο κινητών Α και Β. Οι αρχικές θέσεις είναι 
 Ο
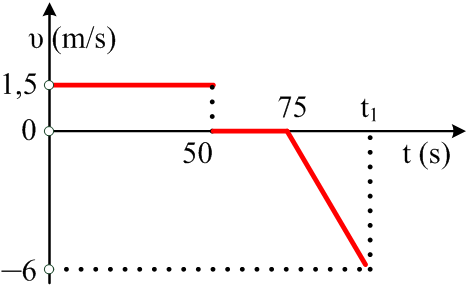
κύριος Διονύσης που έχει βγει στην σύνταξη, σηκώνεται κάθε πρωί να πιει το
καφεδάκι του και μετά πάει στο περίπτερο να αγοράσει την εφημερίδα του. Μιλάει
λίγο με τον περιπτερά και εκείνη τη στιγμή αρχίζει να βρέχει οπότε επιστρέφει
σπίτι του επιταχυνόμενος. Στο διπλανό διάγραμμα φαίνεται η ταχύτητα του Διονύση
σε συνάρτηση με το χρόνο, από την στιγμή που έφυγε από το σπίτι του έως την
επιστροφή του σ’ αυτό.
Ο
κύριος Διονύσης που έχει βγει στην σύνταξη, σηκώνεται κάθε πρωί να πιει το
καφεδάκι του και μετά πάει στο περίπτερο να αγοράσει την εφημερίδα του. Μιλάει
λίγο με τον περιπτερά και εκείνη τη στιγμή αρχίζει να βρέχει οπότε επιστρέφει
σπίτι του επιταχυνόμενος. Στο διπλανό διάγραμμα φαίνεται η ταχύτητα του Διονύση
σε συνάρτηση με το χρόνο, από την στιγμή που έφυγε από το σπίτι του έως την
επιστροφή του σ’ αυτό.


