Σάββατο 26 Δεκεμβρίου 2015
Πέμπτη 24 Δεκεμβρίου 2015
Μια κατακόρυφη κίνηση πριν και μετά το κόψιμο του νήματος.
Ένα σώμα μάζας 0,5kg ηρεμεί στο
έδαφος. Τη στιγμή t=0, δέχεται μέσω νήματος μια κατακόρυφη σταθερή δύναμη μέτρου
F=9Ν, μέχρι τη στιγμή t1=2s, όπου το νήμα σπάει και το σώμα κινείται
πια «ελεύθερα». Αντίσταση του αέρα δεν υπάρχει ενώ g=10m/s2.
i) Να υπολογίστε την επιτάχυνση του σώματος για το
χρονικό διάστημα που στο σώμα ασκείται η δύναμη F.
ii) Πόσο απέχει το σώμα από το έδαφος τη στιγμή που
σπάει το νήμα;
iii) Ποια χρονική στιγμή το σώμα σταματά την ανοδική
του κίνηση; Σε ποιο ύψος βρίσκεται τη στιγμή αυτή;
iv) Να βρεθεί η χρονική στιγμή που το σώμα επιστρέφει
στο έδαφος. Ποια η ταχύτητά του τη στιγμή αυτή;
v) Να γίνουν τα διαγράμματα σε συνάρτηση με το χρόνο:
α) της
ταχύτητας του σώματος, β) της απόστασής
του από το έδαφος.
Κυριακή 20 Δεκεμβρίου 2015
Επιταχυνόμενες κινήσεις σε αντίθετες κατευθύνσεις.
 Δύο αυτοκινητάκια Α1 και Α2 με μάζες
m1
= 3 kg
και m2
= 2 kg
περνούν την χρονική στιγμή t0
= 0 από το ίδιο σημείο του δρόμου που το θεωρούμε ως
x0
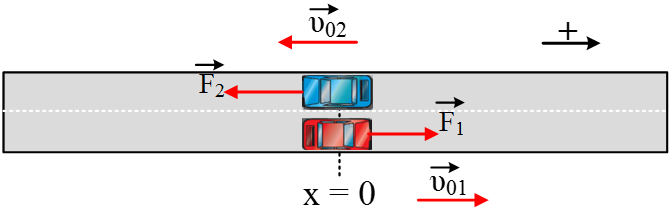
= 0, κινούμενα αντίθετα όπως στο σχήμα, με ταχύτητες μέτρου υ01 = 10
m/s
και υ02 = 4
m/s.
Την ίδια χρονική στιγμή (t0
= 0) ασκούνται στα δύο αυτοκινητάκια δυνάμεις ίδιου μέτρου
F = 12
N
και αντίθετης φοράς ομόρροπες με την κίνηση τους.
Δύο αυτοκινητάκια Α1 και Α2 με μάζες
m1
= 3 kg
και m2
= 2 kg
περνούν την χρονική στιγμή t0
= 0 από το ίδιο σημείο του δρόμου που το θεωρούμε ως
x0
= 0, κινούμενα αντίθετα όπως στο σχήμα, με ταχύτητες μέτρου υ01 = 10
m/s
και υ02 = 4
m/s.
Την ίδια χρονική στιγμή (t0
= 0) ασκούνται στα δύο αυτοκινητάκια δυνάμεις ίδιου μέτρου
F = 12
N
και αντίθετης φοράς ομόρροπες με την κίνηση τους.
α. να βρείτε
τις επιταχύνσεις που αποκτούν τα δύο αυτοκινητάκια
β. να γράψετε
τις εξισώσεις της κίνησης τους
γ. να γράψετε
την εξίσωση που περιγράφει την απόσταση τους κάθε χρονική στιγμή και από εκεί να
υπολογίσετε ποια χρονική στιγμή η απόσταση τους θα είναι
d =
195 m
δ. να γράψετε
την εξίσωση της ταχύτητας για κάθε αυτοκινητάκι και να προσδιορίσετε ποια
χρονική στιγμή τα μέτρα των ταχυτήτων τους θα είναι ίσα
ε. να γίνουν τα
διαγράμματα ταχύτητας χρόνου και θέσης χρόνου για τα δύο αυτοκινητάκια ως την
στιγμή t3
= 5s
στ.
αν την χρονική στιγμή
t0
= 0 οι δυνάμεις που δέχονται τα δύο αυτοκινητάκια ήταν αντίθετες κατεύθυνσης απ’
αυτές που είναι στο σχήμα πόσο διάστημα διανύει το ένα αυτοκινητάκι από την
στιγμή που το άλλο ηρεμεί και μετά;
Πατήστε την εικόνα για την λύση.
Ετικέτες
2. Δυναμική,
Βασίλης Δουκατζής
Σάββατο 19 Δεκεμβρίου 2015
Ακινησία και κίνηση ενός σώματος στο άκρο ελατηρίου.
Το αμαξίδιο του σχήματος ηρεμεί
σε οριζόντιο επίπεδο. Το ιδανικό ελατήριο κρέμεται, δεμένο στο ένα του άκρο, έχοντας
μήκος l0=40cm. Δένουμε στο κάτω άκρο του ένα σώμα Σ1 βάρους
20Ν και το αφήνουμε να ηρεμήσει, οπότε το ελατήριο αποκτά μήκος l1=50cm.
i) Να σχεδιάστε τις δυνάμεις που ασκούνται στο σώμα και να υπολογίστε
τη σταθερά του ελατηρίου.
Σε επανάληψη του πειράματος, το
αμαξίδιο κινείται προς τα δεξιά με σταθερή ταχύτητα υ1=2m/s, ενώ στο
άκρο του ελατηρίου είναι δεμένο ένα δεύτερο σώμα Σ2 βάρους 60Ν, το οποίο
στηρίζεται και στο αμαξίδιο, ενώ το μήκος του ελατηρίου είναι l2=60cm.
ii) Να υπολογίστε
τη δύναμη που ασκεί το σώμα Σ2 στο ελατήριο.
iii) Το σώμα Σ2 δέχεται κάποια δύναμη από
το αμαξίδιο, έστω F1. Αυτή είναι κατακόρυφη ή όχι και γιατί; Να υπολογιστεί
το μέτρο της δύναμης F1.
iv) Σε μια
στιγμή το αμαξίδιο αρχίζει να επιταχύνεται προς τα δεξιά, αυξάνοντας την ταχύτητά
του, χωρίς να γλιστράει πάνω του το σώμα Σ2. Στη διάρκεια της επιτάχυνσης
του αμαξιδίου, το αμαξίδιο ασκεί στο σώμα Σ2 δύναμη:
α) Κατακόρυφη με μέτρο F3=F1.
β) Οριζόντια με κατεύθυνση προς τα δεξιά και μέτρο F3>F1.
γ) Τίποτα από τα παραπάνω.
Δευτέρα 14 Δεκεμβρίου 2015
Ένα εκκρεμές πάνω σε φορτηγό.
Ένα φορτηγάκι κινείται ευθύγραμμα
σε οριζόντιο δρόμο και στο παρακάτω διάγραμμα δίνεται η ταχύτητά του σε συνάρτηση
με το χρόνο.
Πάνω στο φορτηγό έχει στερεωθεί
κατάλληλα ένα στήριγμα, από το οποίο κρέμεται μέσω νήματος ένα σώμα Σ. Στο
παρακάτω σχήμα δείχνει τρεις διαφορετικές θέσεις του νήματος κατά την κίνηση
του φορτηγού, όπου η γωνία που σχηματίζει το
νήμα με την κατακόρυφη διεύθυνση παραμένει σταθερή.
Με βάση το διάγραμμα της ταχύτητας να συμπληρώσετε τον
παρακάτω πίνακα, αντιστοιχώντας τα χρονικά διαστήματα κίνησης με την εικόνα που
δείχνει τη σωστή σχέση του νήματος,
δίνοντας και σύντομες επεξηγήσεις.
Κυριακή 6 Δεκεμβρίου 2015
Ποια στιγμή να καταργήσω την δύναμη;
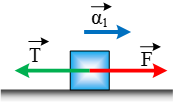 Μικρό
σώμα μάζας
m
= 5 kg βρίσκεται αρχικά ακίνητο σε
οριζόντιο επίπεδο. Η τριβή ολίσθησης μεταξύ του σώματος και του οριζόντιου
επιπέδου έχει μέτρο 20 Ν. Τη χρονική στιγμή t0
= 0 s ασκείται στο σώμα σταθερή οριζόντια δύναμη
F μέτρου ίσο με 50 Ν με
την επίδραση της οποίας το σώμα αρχίζει να κινείται στο οριζόντιο επίπεδο.
Δίνεται ότι η επίδραση του αέρα είναι αμελητέα και η επιτάχυνση της βαρύτητας
είναι
g
= 10 m/ s2.
Να υπολογίσετε:
Μικρό
σώμα μάζας
m
= 5 kg βρίσκεται αρχικά ακίνητο σε
οριζόντιο επίπεδο. Η τριβή ολίσθησης μεταξύ του σώματος και του οριζόντιου
επιπέδου έχει μέτρο 20 Ν. Τη χρονική στιγμή t0
= 0 s ασκείται στο σώμα σταθερή οριζόντια δύναμη
F μέτρου ίσο με 50 Ν με
την επίδραση της οποίας το σώμα αρχίζει να κινείται στο οριζόντιο επίπεδο.
Δίνεται ότι η επίδραση του αέρα είναι αμελητέα και η επιτάχυνση της βαρύτητας
είναι
g
= 10 m/ s2.
Να υπολογίσετε:
α.
το μέτρο της επιτάχυνσης με την οποία κινείται το σώμα,
β.
το ρυθμό μεταβολής της θέσης την χρονική στιγμή
t1
= 2 s,
γ. την χρονική στιγμή t2
που πρέπει να καταργήσουμε την δύναμη F ώστε το σώμα
να σταματήσει την χρονική στιγμή t3
= 15 s
δ. την μέγιστη ταχύτητα κατά την διάρκεια
της κίνησης και την συνολική μετατόπιση.
Πατήστε την εικόνα για την λύση.
Ετικέτες
2. Δυναμική,
Βασίλης Δουκατζής
Δευτέρα 30 Νοεμβρίου 2015
Η κίνηση ενός σώματος μέσα σε ασανσέρ.
Ένα σώμα Σ βάρους 20Ν, ηρεμεί
στο κάτω άκρο ενός ιδανικού ελατηρίου, το οποίο κρέμεται από την οροφή ενός ακίνητου
θαλαμίσκου ασανσέρ, όπως στο σχήμα. Το μήκος του ελατηρίου στην θέση αυτή
είναι 60cm.
i) Αναφερόμενοι στο μήκος του ελατηρίου:
α) Το ασανσέρ
κινείται προς τα πάνω με σταθερή ταχύτητα υ1= 2m/s. Τότε
το μήκος του ελατηρίου θα είναι:
a) 50cm, b) 60cm, c) 70cm.
β) Το ασανσέρ
κινείται προς τα κάτω με σταθερή ταχύτητα υ1= 0,6m/s. Τότε
το μήκος του ελατηρίου θα είναι:
a) 50cm, b) 60cm, c) 70cm.
ii) Αν για να
επιμηκύνουμε το παραπάνω ελατήριο κατά 10cm, απαιτείται να τραβήξουμε το άκρο
του ασκώντας δύναμη 10Ν, να βρεθεί το αρχικό (το φυσικό μήκος) του ελατηρίου. Φυσικό
μήκος του ελατηρίου είναι το μήκος του όταν δεν παραμορφώνεται.
iii) Αν το ασανσέρ κινείται προς τα κάτω με σταθερή
επιτάχυνση α1=2m/s2, να βρεθεί το μήκος του ελατηρίου, αν
την ίδια επιτάχυνση έχει και το σώμα Σ.
iv) Κάτω από το
Σ τοποθετούμε ένα μικρό τραπέζι, πάνω στο οποίο βλέπουμε να στηρίζεται το σώμα
Σ, καθώς το ασανσέρ ανεβαίνει με επιτάχυνση α2=3m/s2. Πόση
δύναμη δέχεται το σώμα από το τραπέζι, αν το μήκος του ελατηρίου είναι l΄=50cm;
Δίνεται g=10m/s2.
Ετικέτες
2. Δυναμική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Σάββατο 28 Νοεμβρίου 2015
Τρία αυτοκίνητα με σταθερές ταχύτητες.
Σε έναν ευθύγραμμο δρόμο
κινούνται τρία αυτοκίνητα Α, Β και Γ με σταθερές ταχύτητες, μέτρων υ1=10m/s, υ2=15m/s και υ3=20m/s,
όπως στο σχήμα.


Κάποια στιγμή, την οποία λαμβάνουμε ως t=0, οι
αποστάσεις των αυτοκινήτων είναι (ΑΒ)=200m και (ΒΓ)=550m. Αφού πάρτε έναν άξονα
x κατά μήκος του δρόμου και ορίστε την αρχή του (x=0), να απαντήσετε στα
παρακάτω ερωτήματα:
i) Ποιες οι αρχικές θέσεις των αυτοκινήτων;
ii) Δώστε την εξίσωση κίνησης κάθε αυτοκινήτου.
iii) Να βρεθούν οι θέσεις των αυτοκινήτων τη στιγμή t1=6s
iv) Να βρεθεί ποια χρονική στιγμή το αυτοκίνητο Γ θα
ισαπέχει από τα άλλα δύο αυτοκίνητα. Ποιες οι θέσεις των αυτοκινήτων τη στιγμή αυτή;
v) Να κάνετε, στο ίδιο σύστημα αξόνων, τις γραφικές
παραστάσεις x-t για κάθε αυτοκίνητο, μέχρι τη χρονική στιγμή t΄=40s.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Τετάρτη 18 Νοεμβρίου 2015
Όσο και αν απομακρυνθείς, θα σε φτάσω!
Ένα αυτοκίνητο Α είναι ακίνητο,
στην άκρη ενός ευθύγραμμου δρόμου. Σε μια στιγμή (ας θεωρήσουμε t0=0),
περνά δίπλα του ένα δεύτερο αυτοκίνητο
Β, το οποίο κινείται με σταθερή ταχύτητα υ2. Την ίδια στιγμή ο οδηγός
του Α, θέτει σε κίνηση το αυτοκίνητό του με σταθερή επιτάχυνση α=1m/s2,
με αποτέλεσμα η απόσταση των δύο αυτοκινήτων να είναι d=72m τη χρονική στιγμή t1=4s.
i) Να βρεθεί η ταχύτητα με την οποία κινείται το Β
αυτοκίνητο.
ii) Ποια η απόσταση των δύο αυτοκινήτων τη στιγμή t2
που έχουν ίσες ταχύτητες;
iii) Να βρεθεί η χρονική στιγμή t3, όπου t3>t2,
κατά την οποία το Β αυτοκίνητο προηγείται
κατά 150m του Α. Σε ποιες θέσεις βρίσκονται τη στιγμή αυτή τα δυο οχήματα;
iv) Αν τη στιγμή t3 το Α αυτοκίνητο σταματά
να επιταχύνεται, κινούμενο πλέον με σταθερή ταχύτητα, ποια χρονική στιγμή t4,
τα δυο αυτοκίνητα, θα βρεθούν το ένα δίπλα στο άλλο και σε πόση απόσταση από
την αρχική θέση θα συμβεί αυτό;
v) Να κάνετε στο ίδιο διάγραμμα τις γραφικές παραστάσεις
για τις θέσεις των δύο αυτοκινήτων σε συνάρτηση
με το χρόνο (x-t), μέχρι τη στιγμή t4.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Πέμπτη 12 Νοεμβρίου 2015
Δουλεύοντας με ένα διάγραμμα θέσης.
Ένα σώμα κινείται ευθύγραμμα
και στο διπλανό διάγραμμα δίνεται η γραφική παράσταση της θέσης του, σε συνάρτηση
με το χρόνο. Με διαφορετικά χρώματα, έχουν χαραχθεί τα τμήματα που αντιστοιχούν
σε διαφορετικές κινήσεις. Στα χρονικά διαστήματα που η ταχύτητα μεταβάλλεται, η
μεταβολή αυτή πραγματοποιείται με σταθερό ρυθμό.
i) Να περιγράψετε
τις κινήσεις που πραγματοποιεί το σώμα, στα διάφορα χρονικά διαστήματα. Για πόσο
χρονικό διάστημα κινήθηκε συνολικά το σώμα;
ii) Να υπολογιστεί η ταχύτητα του σώματος τη στιγμή t2=3s.
iii) Να βρεθεί η επιτάχυνση του σώματος, στα χρονικά
διαστήματα όπου μεταβάλλεται η ταχύτητα.
iv) Να υπολογιστούν οι τιμές της θέσης β και γ τις χρονικές
στιγμές 4s και 6s.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Κυριακή 1 Νοεμβρίου 2015
Μα τι κίνηση κάνει επιτέλους αυτό το κινητό;

Ένα αυτοκίνητο που κινείται σε άξονα έχει ταχύτητα
υ0 = +15 m/s και τη στιγμή t0 = 0 περνάει από τη θέση
χ0 = 0. Με την ταχύτητα υ0 κινείται για 5 s και στη συνέχεια κινείται με επιτάχυνση -3 m/s2 για το χρονικό διάστημα 5 s – 15 s. Τέλος για το χρονικό διάστημα 15 s – 25 s επιταχύνεται με επιτάχυνση 1,5 m/s2.
υ0 = +15 m/s και τη στιγμή t0 = 0 περνάει από τη θέση
χ0 = 0. Με την ταχύτητα υ0 κινείται για 5 s και στη συνέχεια κινείται με επιτάχυνση -3 m/s2 για το χρονικό διάστημα 5 s – 15 s. Τέλος για το χρονικό διάστημα 15 s – 25 s επιταχύνεται με επιτάχυνση 1,5 m/s2.
α) Να γίνει το διάγραμμα α→t
β) Να βρείτε τη θέση του αυτοκινήτου και την ταχύτητα στο τέλος κάθε
φάσης της κίνησης.
γ) Ποιο είναι το συνολικό διάστημα που διανύει το αυτοκίνητο;
δ) Να γίνουν τα διαγράμματα χ→t
και υ →t.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 3.,
Ανδρέας Ριζόπουλος
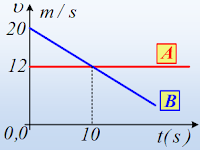
Δύο ευθύγραμμες κινήσεις και διαγράμματα.
Σε ευθύγραμμο δρόμο κινούνται δύο
κινητά Α και Β. Κάποια στιγμή (t0=0) τα δύο κινητά περνούν από την ίδια
θέση Ο (έστω x=0) και στο διπλανό διάγραμμα φαίνονται οι ταχύτητές τους σε συνάρτηση
με το χρόνο.
i) Να υπολογίσετε
τις επιταχύνσεις των δύο σωμάτων.
ii) Να γράψετε την εξίσωση θέσης (x-t) για κάθε κινητό.
iii) Πόσο απέχουν μεταξύ τους τα δύο κινητά τη στιγμή
που έχουν ίσες ταχύτητες;
iv) Να βρεθεί η χρονική στιγμή που το Β κινητό σταματά,
αν παύει να κινείται μόλις μηδενιστεί η ταχύτητά του.
v) Σε ποιο από τα παρακάτω σχήματα, έχουν σχεδιαστεί
σωστά οι γραφικές παραστάσεις x-t για τα δυο σώματα, μέχρι τη στιγμή t΄=30s; Να
δικαιολογήστε την επιλογή σας, αφού εξηγείστε γιατί απορρίπτετε τα υπόλοιπα.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Τρίτη 27 Οκτωβρίου 2015
Από φανάρι σε φανάρι.
Ένα αυτοκίνητο είναι σταματημένο στο φανάρι που είναι «κόκκινο». Τη στιγμή που ανάβει το «πράσινο», έστω t0=0, το αυτοκίνητο μαρσάρει, οπότε αποκτά σταθερή επιτάχυνση με αποτέλεσμα τη χρονική στιγμή t1=8s να έχει ταχύτητα υ1=24m/s. Στη συνέχεια συνεχίζει με σταθερή ταχύτητα, μέχρι να φτάσει στο επόμενο «πράσινο» φανάρι, που απέχει s=240m από το προηγούμενο.
i) Να βρείτε την επιτάχυνση με την οποία κινήθηκε στο χρονικό διάστημα 0-t1.
ii) Πόσο απέχει από το πρώτο φανάρι (όπου θεωρούμε ότι xο=0) το αυτοκίνητο, τη στιγμή που παύει να επιταχύνεται;
iii) Ποια στιγμή φτάνει το όχημα στο δεύτερο φανάρι;
iv) Να κάνετε τις γραφικές παραστάσεις της ταχύτητας και της θέσης του κινητού σε συνάρτηση με το χρόνο, θεωρώντας x=0 τη θέση του πρώτου φαναριού.
v) *Αν το 2ο φανάρι γίνεται πορτοκαλί τη στιγμή t΄=13s και το αυτοκίνητο φτάνει σε αυτό τη στιγμή αλλαγής του χρώματος, ενώ κινήθηκε αρχικά με την ίδια επιτάχυνση, όπως προηγούμενα, μέχρι να αποκτήσει μια ταχύτητα υ2, με την οποία συνέχισε την κίνησή του, να υπολογιστεί το χρονικό διάστημα επιτάχυνσής του και η τελική του ταχύτητα.
*Ερώτημα μόνο για καλούς μαθητές.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Τρίτη 20 Οκτωβρίου 2015
Πληροφορίες από μερικά διαγράμματα.
1) Σε ευθύγραμμο
δρόμο κινούνται τρία σώματα Α, Β και Γ και στο σχήμα φαίνονται οι θέσεις τους σε
συνάρτηση με το χρόνο.
Χαρακτηρίστε
ως σωστές ή λανθασμένες τις παρακάτω προτάσεις, δίνοντας σύντομες εξηγήσεις.
i) Μεγαλύτερη μετατόπιση μέχρι τη στιγμή t2 έχει το Α σώμα.
ii) Τα σώματα Α και Β μετατοπίζεται το ίδιο στο χρονικό
διάστημα 0-t1.
iii) Τα σώματα Α και Β μετατοπίζεται το ίδιο στο
χρονικό διάστημα 0-t2.
iv) Μέχρι τη στιγμή t2 οι μετατοπίσεις των
σωμάτων Β και Γ είναι ίσες.
iv) Τη στιγμή της συνάντησης των τριών σωμάτων, οι ταχύτητές
τους είναι ίσες.
2) Σε ευθύγραμμο
δρόμο κινούνται δύο σφαίρες Α και Β και
στο σχήμα φαίνονται οι θέσεις τους σε συνάρτηση με το χρόνο.
i) Πάνω στο σχήμα να σχεδιάστε το διάνυσμα της ταχύτητας
της σφαίρας Β.
ii) Στο σχήμα βλέπετε τις θέσεις των σφαιρών κάποια
στιγμή t΄. Αυτή η χρονική στιγμή είναι πριν ή μετά τη στιγμή t1;
iii) Να συγκρίνετε τα μέτρα των ταχυτήτων των δύο
σφαιρών.
Δείτε τη συνέχεια….
ή
Ετικέτες
1. Κινηματική,
9. Επίπεδο 2.,
Διονύσης Μάργαρης
Κυριακή 18 Οκτωβρίου 2015
Μελέτη ενός διαγράμματος επιτάχυνσης.
Ένα αρχικά ακίνητο σώμα, αρχίζει να κινείται ευθύγραμμα τη στιγμή t=0 και στο διάγραμμα δίνεται η επιτάχυνσή του, σε συνάρτηση με το χρόνο.
i) Να περιγράψετε την κίνηση του σώματος στα διάφορα χρονικά διαστήματα, που εμφανίζονται στο διάγραμμα, θεωρώντας την προς τα δεξιά κατεύθυνση ως θετική.
ii) Ποια χρονική στιγμή στο χρονικό διάστημα από 0-3s το σώμα έχει την μέγιστη κατά μέτρο ταχύτητα;
iii) Να υπολογίσετε τη μεταβολή της ταχύτητας στο χρονικό διάστημα 0-2s.
iv) Να υπολογιστεί η ταχύτητα του σώματος τη στιγμή t2=3s.
v) Ποια χρονική στιγμή το σώμα θα σταματήσει την προς τα δεξιά κίνησή του και θα αρχίσει να κινείται προς τα αριστερά; Να βρεθεί η ταχύτητά του τη στιγμή t΄=8,3s.
Ετικέτες
1. Κινηματική,
9. Επίπεδο 3.,
Διονύσης Μάργαρης
Εγγραφή σε:
Αναρτήσεις (Atom)